2的约数有( );
1的约数有( );
4的约数有( );
18的约数有( );
33的约数有( );
6的约数有( )。
根据约数个数的情况,可以把这几个数分成几类?
(板书)
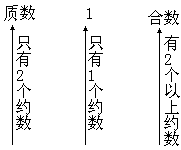
只有2个约数,也就是除了1和它本身以外,不再有别的约数,这个数叫什么?
什么叫合数?1是质数还是合数?
找一找,你们手里的数字卡片有质数吗?举起来。有合数吗?举起来。
谁既不是质数,也不是合数?举起来。
(三)练习
1.判断题。(对的画“√”,错的画“×”)
(1)一个合数至少有三个约数。 ( )
(2)一个质数与2的和一定是奇数。 ( )
(3)两个质数相乘的积一定是合数。 ( )
2.选择题。
(1)下面三个数中既是奇数又是质数的数是 [ ]。
A.43
B.9
C.51
(2)下面三个数中是偶数而不是质数的数是 [ ]。
A.14
B.47
C.2
(3)最小的质数与最小的合数的积是 [ ]。
A.6
B.8
C.4
看来我们做上面题时,要想正确迅速地选择^答~`案,不但20以内的质数要熟,而且百以内的质数表也要熟。百以内的质数有多少个?
(学生起立,边拍手边背百以内质数的顺口溜。)
二,三,五,七,一十一;
一三,一九,一十七;
二三,二九,三十七;
三一,四一,四十七;
四三,五三,五十九;
六一,七一,六十七;
七三,八三,八十九;
再加七九,九十七;
25个质数不能少;
百以内质数心中记。
(四)总结
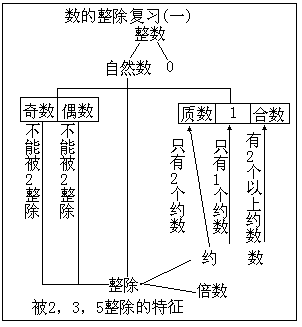
这节课我们复习了数的整除的一部分知识,并用网络图表示出来了。谁能把各部分知识之间的联系说说?
同学们总结得很好,请打开书。
1.做书上的练习。
2.补充题。
判断:(对的画“√”,错的画“×”。)
(1)奇数都是质数。 ( )
(2)偶数都是合数。 ( )
(3)一个数的约数总比这个数的倍数小。 ( )
(4)15×12的积一定能同时被2,3,5整除。 ( )
(5)两个不同的奇数的和是合数。 ( )
(6)10以内质数和是1+2+3十5+7+9=27。 ( )
(7)一个除法算式只要商是整数,没有余数就叫整除。 ( )
课堂教学设计说明
本节课是根据整除这部分知识之间的内在联系而精心设计的。边复习边板书,边复习知识点边练习,最后使学生形成知识网络。
第一步:通过6道除法式题,用集合圈逐层分类,复习了整除的概念,明确了整除和除尽的关系,以及约数、倍数的概念。
第二步:复习整数和自然数的概念,明确我们现在研究数的整除是在自然数范围研究的。自然数按能否被2整除而分为奇数和偶数;按照约数的个数分,分为质数、合数和1。
第三步:根据知识之间的内在联系,做综合练习,使学生灵活地运用所学的知识解决问题。
板书设计